Have you ever wondered how artists create the illusion of movement in their artwork? Or how special effects in movies make objects appear to fly or shrink? The answer lies in the fascinating world of geometric transformations. These transformations act like magic wands, altering the shape, size, and position of objects, creating captivating visual effects.
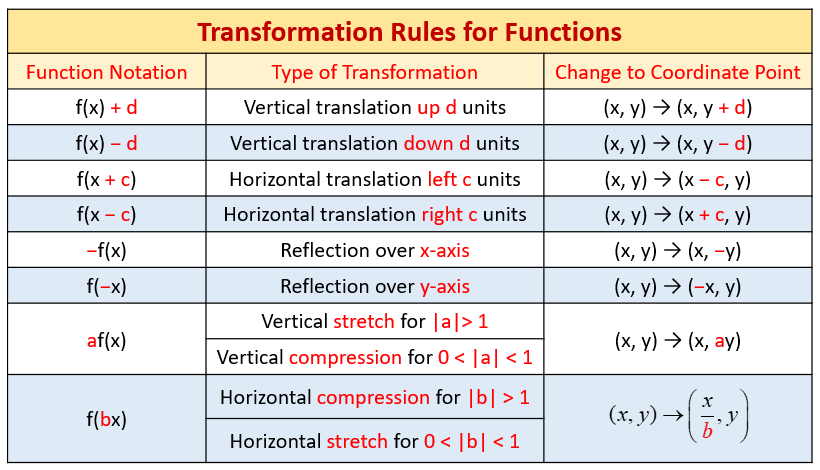
Image: www.onlinemathlearning.com
Just the other day, I was sketching a landscape, and I wanted to make the distant mountains appear smaller. That’s when I realized I could use a dilating transformation to compress the mountains vertically, creating a sense of distance. It was such a simple concept, yet it completely changed the look of my drawing!
Understanding Geometric Transformations
What are Geometric Transformations?
Geometric transformations are mathematical operations that manipulate the position, size, and orientation of geometric figures. They are a fundamental concept in geometry and have applications in various fields, including computer graphics, animation, and even robotics.
Geometric transformations can be categorized into four basic types:
- Translation: Shifting a figure from one location to another without changing its shape or size.
- Rotation: Spinning a figure around a fixed point called the center of rotation.
- Reflection: Flipping a figure across a line called the line of reflection.
- Dilation: Scaling a figure up or down, changing its size but preserving its shape.
How Transformations Work
Understanding how transformations work involves visualizing the effects of these operations on a figure. Each transformation is applied to every point of the figure, resulting in a new set of points that define the transformed figure.
For example, in a translation, every point of the original figure is moved a fixed distance in the same direction. Similarly, in a rotation, each point is rotated around the center of rotation by a specific angle.
These transformations can be represented mathematically using matrices, which provide a concise and powerful way to perform complex geometric manipulations.
![How to Teach Graphing Transformations of Functions [Hoff Math]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjXryPzh55_HG7TSDpeht0tz6N0Dme7v37J5P1gFEzPLGR6h7BDWzn94_BCavsHgdeZ2R4Z7_pjNvPnzg3eHGc1bJ8tZzyeAKbgHtuv4cWDOaGp2TaTMXHV9ZF13wuXcDepuEzPjYYQHnqxWhhum5MMQEuDSMfopiQCvOsBLbdo9ZGoCcCljU3cQg/s1280/chart for graphing transformations.jpg)
Image: www.hoffmath.com
Graphing Transformations in Practice
Let’s delve into how to graph the image of a given figure using the specified transformations. We’ll examine each transformation in detail and demonstrate how to apply them graphically.
Translation
To translate a figure, we move each point of the figure a fixed distance in the same direction. This direction is typically represented by a vector, denoted as (h, k).
To graph the translation of a figure, we add the horizontal component (h) to the x-coordinate of each point and the vertical component (k) to the y-coordinate. This effectively shifts the figure to a new location.
Rotation
Rotating a figure around a point involves spinning it by a specific angle. The center of rotation acts as the pivot point, and the angle of rotation determines the amount of rotation.
Graphing a rotation involves finding the image of each point after applying the rotation. This can be done by using trigonometric formulas to calculate the new coordinates or by using a protractor to measure the angle of rotation.
Reflection
Reflecting a figure across a line is like creating a mirror image. The line of reflection acts as the mirror, and the image of the figure is a symmetrical copy reflected across this line.
Graphing a reflection involves finding the image of each point of the figure with respect to the line of reflection. This can be done by drawing perpendicular lines from each point to the line of reflection and extending them the same distance on the opposite side.
Dilation
Dilating a figure involves scaling its size up or down. The scale factor, denoted by k, determines the size change. If k is greater than 1, the figure is enlarged, and if k is less than 1, the figure is shrunk.
Graphing a dilation involves multiplying the coordinates of each point of the figure by the scale factor. This effectively changes the distance of each point from the origin by a factor of k.
Tips for Graphing Transformations
Here are some tips to make graphing transformations easier and more accurate:
- Start with a clear understanding of the transformation: Review the definition of the transformation and familiarize yourself with its effects.
- Choose an appropriate scale: Ensure the chosen scale on your graph allows for clear representation of the figure and its image.
- Use a ruler and protractor: Accuracy is key in graphing transformations. Use measuring tools to ensure precise measurements of distances and angles.
- Label your points and figures: Clearly label the original figure, the transformation, and any relevant points to avoid confusion.
- Practice, practice, practice: The more you practice graphing transformations, the better your understanding and skills will become.
FAQs about Graphing Transformations
Q: Can I combine multiple transformations on a figure?
A: Absolutely! You can combine multiple transformations to create complex visual effects by applying them sequentially. The order of applying transformations usually affects the final result.
Q: What are some real-world applications of geometric transformations?
A: Transformations play a crucial role in computer graphics, animation, and design. They are used to move, resize, rotate, and scale objects in virtual environments, creating realistic and dynamic images and animations.
Q: Are there any online tools that can help with graphing transformations?
A: Yes, there are numerous online tools and software applications designed to help visualize and graph geometric transformations. These tools offer an interactive approach to exploring the concepts and visualizing the results of different transformations.
Graph The Image Of The Figure Using The Transformation Given
Conclusion
Graphing transformations is a fundamental skill in geometry and has vast applications in various fields. From computer graphics to art and even robotics, the ability to manipulate geometric figures through transformations is essential. By understanding the concepts and practicing graphing techniques, you can create captivating visuals and explore the world of geometry in a whole new light.
Are you interested in learning more about specific transformations or exploring their applications in real-world scenarios? Share your thoughts in the comments below!






