Remember that awkward moment in high school when you were trying to figure out the whole “dating” thing? You’d meet someone, get a little excited, and then realize…they weren’t really interested in the same way you were? That’s kind of like the beginning of understanding relationships in mathematics. We have these concepts called “relations” where we see if there’s a connection between two sets of things, but it’s not always a perfect match. And then there are “functions,” which are basically the “stable relationships” – all elements in one set neatly paired with exactly one element in another. But don’t worry, understanding these concepts is less complicated than the drama of teenage dating!
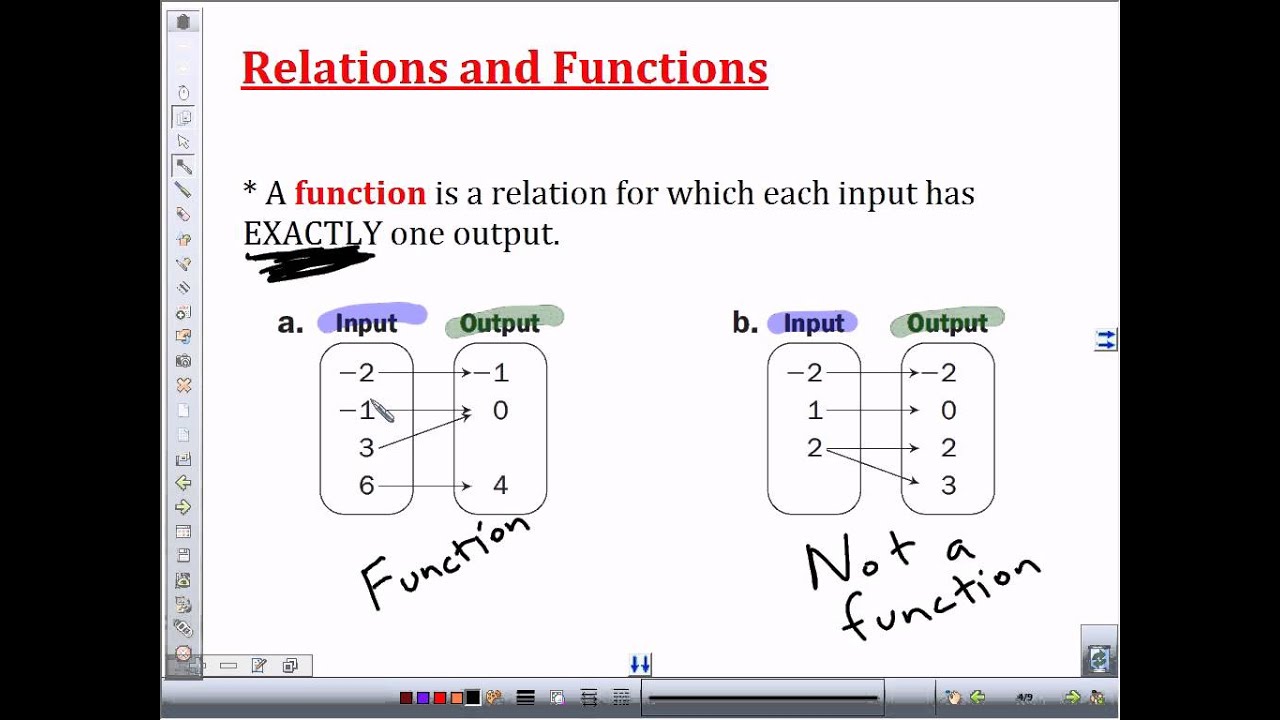
Image: www.youtube.com
This article will delve into the world of 2:1 relations and functions, where we’ll explore the specific characteristics of these relationships and how they differ from one another. We’ll also equip you with practical practice tips and tricks to master these concepts. Get ready to unravel the secrets of mathematical connections!
Defining Relationships: Relations and Functions
Let’s start with the basics. A **relation** in mathematics is simply a way of showing how elements in one set relate to elements in another. Imagine you have two sets: Set A is the set of all your favorite colors and Set B is the set of all your favorite fruits. A relationship could be “Your favorite color is the same as your favorite fruit.” You might pair “red” with “strawberry” and “green” with “kiwi” – and those would be your “related” pairs.
A **function**, however, is a special type of relation. In a function, every element in the first set (called the domain) is paired with **exactly one** element in the second set (called the range). So, in our example, you couldn’t have “red” paired with both “strawberry” and “apple” – that would break the function rule.
Visualizing the Differences
Here’s a simple way to visualize this:
| Type of Relationship | Characteristics | Visualization |
|---|---|---|
| Relation | Elements in a set can be paired with one or more elements in another set. | A collection of arrows pointing from one set to another, with arrows possibly starting or ending at the same point. |
| Function | Every element in the first set (domain) is paired with exactly one element in the second set (range). | A collection of arrows pointing from one set to another, where each element in the first set has exactly one arrow pointing from it. |
Understanding 2:1 Relations and Functions
The term “2:1” specifically refers to a relationship or function where two elements in the first set are paired with a single element in the second set. Think of it as a “two-to-one” connection. Here’s an example:
Let’s say Set A is the set of all students in a class: Alice, Bob, Charlie, David
And Set B is the set of all their favorite pets: Cat, Dog
Here’s a 2:1 relation: Alice and Bob both have cats as their favorite pet, Charlie has a dog, and David also has a dog. Here, two students are “paired” with one type of pet.
In a 2:1 function, however, this wouldn’t be allowed. Every student must have a unique favorite pet. So, for example, we could have: Alice and Charlie both have cats, Bob and David both have dogs. In this case, each student is paired with only one unique favorite pet.

Image: www.functionworksheets.com
Practice Makes Perfect
The key to grasping these concepts is practice. Don’t just memorize the definitions – work through examples and see how the concepts are applied. Here’s how you can practice:
1. Use Diagramming Techniques
Draw arrows or mappings between elements in sets to visualize relations and functions. This will help you see the connections clearly.
2. Create Your Own Scenarios
Come up with real-life examples of 2:1 relations and functions. This will make the concepts more relatable and engaging. What are some real-world scenarios where you might see a “two-to-one” connection?
3. Practice with Equations
Learn to represent relations and functions using equations, and practice solving for specific values.
Top Tips for Mastering 2:1 Relations and Functions
Here’s a quick recap of our practice tips, along with some additional advice:
1. Focus on Clarity:
Remember, clarity is key. Make sure you understand the difference between relations and functions, and really grasp the “two-to-one” concept of 2:1 relations and functions.
2. Don’t Overcomplicate:
Keep it simple. Too many complicated examples will only add to the confusion.
3. Embrace Visuals:
Use diagrams and visualizations to understand the relationships between sets. It’s like those “relationship diagrams” where people connect the dots to understand families!
FAQs
Q: Can a 2:1 relation be a function?
A: No, a 2:1 relation cannot be a function. A function requires that every element in the domain is paired with exactly one element in the range. In a 2:1 relation, two elements are paired with a single element.
Q: How can I determine if a given relation is a 2:1 relation?
A: Look for instances where two elements in the first set are paired with a single element in the second set.
Q: Are 2:1 relations always functions?
A: No, 2:1 relations are never functions. The core concept of a function is the unique mapping of each input to exactly one output.
2 1 Relations And Functions Practice
Conclusion:
So, there you have it! We’ve broken down the world of 2:1 relations and functions. Remember, understanding these concepts is about recognizing those mathematical relationships – like seeing the match (or mismatch ) in a “dating game” of sets! We hope this article has helped you feel more confident in tackling these concepts. Keep practicing, keep exploring, and keep your mathematical mind sharp!
Are you interested in learning more about relations and functions, or would you like to explore other mathematical concepts? Let us know in the comments below!






