Have you ever stared at a trigonometry worksheet, feeling overwhelmed by a sea of sine, cosine, and tangent? The world of trigonometry can seem daunting at first, but with the right approach, it can become a fascinating journey into the relationships between angles and sides of triangles. This guide will delve into the world of trigonometric ratios, equip you with the tools to tackle any worksheet, and empower you to confidently navigate the intricacies of this essential branch of mathematics.
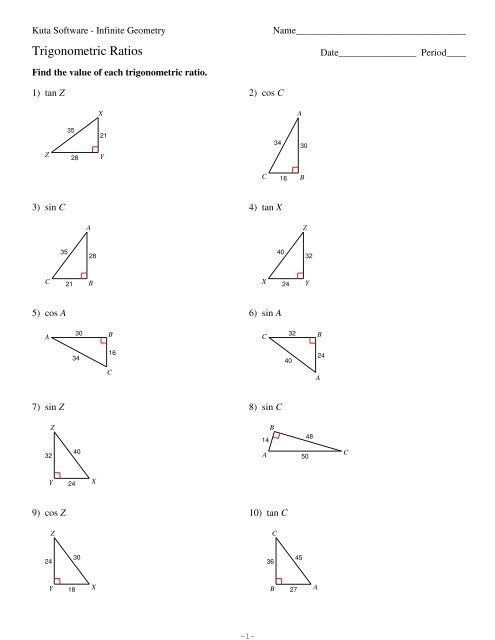
Image: studylistkrueger.z13.web.core.windows.net
Trigonometric ratios form the backbone of understanding angles and their connections to the lengths of sides in triangles. They are the building blocks for solving a wide range of problems, from calculating the height of a tall building to determining the trajectory of a projectile. This guide aims to demystify these ratios, giving you the knowledge and confidence to tackle any trigonometric ratio worksheet with ease.
Understanding the Basics: Sine, Cosine, and Tangent
At the heart of trigonometry are three fundamental ratios: sine (sin), cosine (cos), and tangent (tan). To understand these ratios, we need to picture a right-angled triangle. Let’s label the sides:
- Hypotenuse: The longest side, opposite the right angle.
- Opposite: The side opposite the angle we’re interested in.
- Adjacent: The side next to the angle we’re interested in.
Now, here’s how sine, cosine, and tangent are defined:
- Sine (sin): sin (angle) = Opposite / Hypotenuse
- Cosine (cos): cos (angle) = Adjacent / Hypotenuse
- Tangent (tan): tan (angle) = Opposite / Adjacent
Remember the acronym SOH CAH TOA to help you remember these ratios:
- Sine = Opposite / Hypotenuse
- Cosine = Adjacent / Hypotenuse
- Tangent = Opposite / Adjacent
Mastering the Basics: Solving for Trigonometric Ratios
Let’s put these ratios into practice with a simple example. Imagine a right-angled triangle where the angle we’re interested in is 30 degrees. The opposite side is 5 cm, and the hypotenuse is 10 cm.
To find the sine of 30 degrees:
- sin (30°) = Opposite / Hypotenuse = 5 cm / 10 cm = 1/2
To find the cosine of 30 degrees:
- *cos (30°) = Adjacent / Hypotenuse = √3 5 cm / 10 cm = √3 / 2**
To find the tangent of 30 degrees:
- *tan (30°) = Opposite / Adjacent = 5 cm / (√3 5 cm) = 1/√3 = √3 / 3**
These calculations illustrate how to use the definitions of sine, cosine, and tangent to determine the values of these ratios for a given angle in a right-angled triangle.
Beyond the Basics: The Unit Circle and Special Angles
To delve deeper into the world of trigonometric ratios, we need to introduce the unit circle. The unit circle is a circle with a radius of 1 unit centered at the origin of a coordinate plane. It’s a powerful tool for visualizing and understanding trigonometric functions.
Imagine a point on the unit circle, and draw a line from that point to the origin. This line forms the hypotenuse of a right-angled triangle. The x-coordinate of the point represents the cosine of the angle, and the y-coordinate represents the sine of the angle.
The unit circle also helps us understand the trigonometric ratios of special angles like 0°, 30°, 45°, 60°, and 90°. These angles have specific trigonometric values that are often used in problem-solving. You can find these values in tables or derive them using geometric principles.
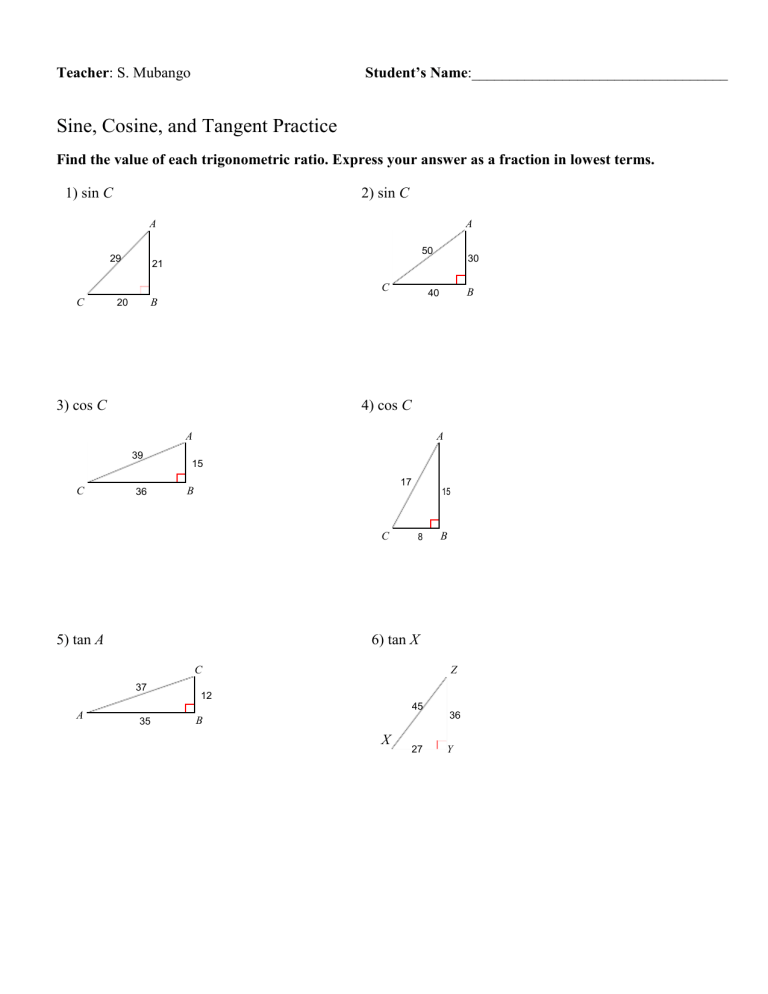
Image: possessivenounsworksheets.blogspot.com
Tackling Trigonometric Ratio Worksheets
Now, let’s equip you with the tools to conquer any trigonometric ratio worksheet. Here’s a step-by-step approach:
-
Identify the angle and the given sides: Look at the triangle provided in the problem. Note the angle you’re working with and identify which sides are given (opposite, adjacent, or hypotenuse).
-
Choose the appropriate trigonometric ratio: Based on the given sides, select the trigonometric ratio that relates those sides to the angle. Remember SOH CAH TOA to guide your choice.
-
Set up the equation: Write the equation using the selected trigonometric ratio and the given sides.
-
Solve for the unknown: Use algebraic manipulation to solve for the unknown side or angle.
-
Check your answer: Verify your answer by using the Pythagorean Theorem or other trigonometric identities.
Mastering the Art of Trigonometry: Expert Insights and Actionable Tips
Trigonometry is a core concept in various fields, including physics, engineering, and astronomy. Understanding these ratios is essential for successful problem-solving in these areas.
Here are a few actionable tips from seasoned mathematicians:
-
Practice makes perfect: The more you practice solving trigonometric ratio problems, the more comfortable you’ll become with the concepts.
-
Visualize the concepts: Draw diagrams and visualize the relationship between angles and sides to solidify your understanding.
-
Use technology: Utilize calculators and online resources to assist with calculations and explore different trigonometric concepts.
-
Don’t be afraid to ask for help: If you encounter difficulties, don’t hesitate to seek help from teachers, tutors, or online resources.
Find The Value Of Each Trigonometric Ratio Worksheet Answer Key
Conclusion
Navigating the world of trigonometry can be an empowering experience, providing you with the tools to solve problems and understand the intricate relationships between angles and sides. This guide has equipped you with the knowledge and strategies to tackle trigonometric ratio worksheets confidently. Remember to keep practicing, visualize the concepts, and don’t be afraid to explore additional resources. The journey into the fascinating world of trigonometry awaits!






