In the realm of digital circuits, efficiency is paramount. We strive to design circuits that perform their intended functions while minimizing the number of components and power consumption. Imagine trying to build a complex circuit with hundreds of gates – not only would it be bulky, but it would also be extremely prone to errors and slow down operations. Thankfully, tools like Karnaugh mapping come to our rescue!

Image: mavink.com
My own foray into the world of Karnaugh maps started in my college electronics class. I was struggling to simplify a complex Boolean expression, but after learning about Karnaugh maps, a whole new world opened up. This method, developed by Maurice Karnaugh in 1953, revolutionized the way we approach circuit design by providing a visual and intuitive means of simplifying Boolean expressions.
Understanding Karnaugh Maps
Karnaugh maps, often called K-maps, are a visual representation of Boolean functions. They use a grid-like structure to depict the relationship between input variables and the output of the function. Each cell in the K-map corresponds to a unique combination of input variables. The beauty of K-maps lies in their ability to highlight adjacent cells representing minterms that can be combined to simplify the Boolean expression.
Let’s delve into the basics to understand their magic. Imagine you have a Boolean function with ‘n’ input variables. A K-map for this function will have 2n cells, each representing a unique combination of input values. The cells are arranged in a way that adjacent cells differ by only a single input variable. This arrangement makes it super easy to spot groups of adjacent ‘1’s in the map, which represent terms that can be simplified.
Steps Involved in Karnaugh Map Simplification
1. Creating the Karnaugh Map:
The first step is to create the K-map based on the Boolean expression. To do this:
* **Identify the number of input variables:** This determines the size of the K-map. For example, a function with three input variables (A, B, C) will have a 2<sup>3</sup> = 8-cell K-map.
* **Label the rows and columns:** The rows and columns are labeled with binary codes representing the input variables. The labels are chosen in a way that adjacent cells differ by only one bit. This ensures that adjacent cells differ in only one input variable.
* **Fill in the cells:** Each cell corresponds to a specific combination of inputs. The cell value is set to '1' if the Boolean expression is True for that input combination and '0' if it's False. </p>
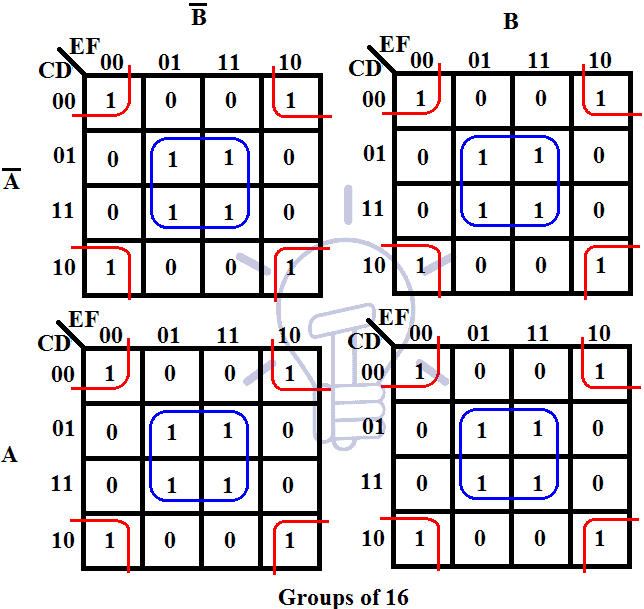
Image: mappingmemories.ca
2. Identifying Groups of Adjacent One’s:
Once the K-map is filled, the next step is to identify groups of adjacent 1’s. These groups must consist of 2n adjacent ‘1’s, where n is a non-negative integer. For example, you can have groups of 2, 4, 8, and so on.
3. Writing the Simplified Boolean Expression:
To derive the simplified Boolean expression, we need to consider the groups of adjacent ‘1’s we identified in the previous step. For each group, the simplified term corresponds to the common variables that are the same for all cells within the group. We then use the OR operation to combine the simplified terms for each group. This process effectively eliminates redundant terms and simplifies the original Boolean expression.
Tips and Expert Advice
Here’s a pro tip when working with Karnaugh maps: Always make sure your groups are as large as possible. This helps to minimize the number of terms in the final expression. Try to form groups of 4, 8, or even 16 cells whenever possible. If you’re not sure about some cells, mark them as ‘don’t care’ values represented by ‘X.’ They can be helpful for creating larger groups.
Remember, practice makes perfect! Working through different examples and understanding the various scenarios will make you an expert in using Karnaugh maps for circuit simplification.
Frequently Asked Questions
Q1: What are the advantages of using Karnaugh maps for circuit simplification?
A1: Karnaugh maps offer several advantages over traditional algebraic simplification methods. They are:
* **Visual and Intuitive:** K-maps provide a visual representation of the Boolean expression, making it easy to identify groups of adjacent 1's and simplify the expression.
* **Efficient:** They offer a faster and more efficient method of simplifying complex Boolean expressions, eliminating the need for tedious algebraic manipulations.
* **Error-Prone:** They reduce the chances of human errors that can occur during algebraic simplification.Q2: Can I use Karnaugh Maps for functions with more than 4 input variables?
A2: While Karnaugh maps are highly effective for functions with up to four input variables, handling functions with more input variables becomes quite challenging and less intuitive visually. For such cases, other methods like the Quine-McCluskey algorithm or computer-aided design tools are preferred.
Activity 2.2.1 Circuit Simplification Karnaugh Mapping
Conclusion
Karnaugh maps have revolutionized the process of simplifying Boolean expressions, leading to more efficient and robust digital circuits. Understanding and utilizing this visual method is crucial for anyone working with digital logic design. So, if you find yourself struggling with simplifying Boolean expressions, remember – Karnaugh maps are your friend!
Are you interested in learning more about this powerful technique? If so, let us know in the comments below!






